（はじめに）準周期的な並進秩序とは？

1次元の逆格子空間を考える。
周期的な並進秩序とは、逆格子ベクトルを成す基本ベクトル同士の比が、 有理数であるものから成る。 例えば、g1 ,g2なる基本ベクトルがあり、g1/g2 が有理数であるときが該当する。 このとき、逆格子ベクトルGは、整数n，mを用いて、
G=n*g1 + m*g2

一方で、比g1/g2が無理数であるとき、非周期的であると呼ぶ。 準周期的な並進秩序であるとは、非周期的であることに加えて、基本ベクトルが有限個である 場合を指す。
上記の　G=n*g1 + m*g2　において、比g1/g2が無理数であるならば、準周期的であると 呼ぶ。
アモルファスの逆格子空間の基本ベクトルは、連続的な値をとりうるが、 これは非周期的と呼ぶ。

準結晶とは？

以下を満たす固体を、”準結晶”と定義する。
（１）準周期的な並進秩序がある。
（２）逆格子空間において、通常の結晶で許されない回転対称性（8回・10回・12回）を持つ。


歴史的な話は、以下のページにまとめた。
歴史的なこと

準結晶の構造を理論的に取り扱うとき、準周期的な配置が出発点になる。 離散的・連続的に取り扱われている。
離散的な扱いは、”Cut法”などがある。連続的には弾性論や流体力学的な扱いをしている。

Cut法とフェイゾン

準周期的な並進秩序を持った格子を得るには、”Cut法”という方法がある。
まず、実際の格子が存在する空間より高次の空間を仮定する。この空間を”超空間”と 名づけ、周期的な格子であるとする。ここで、超空間の次元を2次元とし、実際の空間を 1次元として、話を進める。
超空間の格子内の異なる2点を適当に結ぶ直線を考える。 これは、超空間の格子に対して、有理数の傾きを持つ直線を引くことに対応する。 この線に格子点を射影すると、周期的な並進秩序を持った格子が得られる。

一方で、無理数の傾きを持つ直線を引き、射影すると、射影した点が実際の空間に 稠密に詰まる。これは、連続した点の集まりになるが、このとき射影される格子点を 適当な幅の中の格子点に制限すると、準周期的な並進秩序を持った点が得られる。

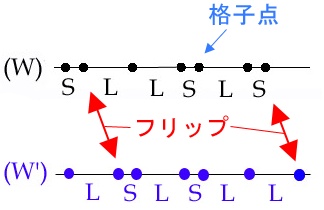
フェイゾンフリップに関して

本研究に関して

本研究では、準結晶に特有なフリップ現象を取り扱う。 これは、原子の位置が局所的に飛び移る現象であり、フェイゾンが起因していると 言われている。 そこで、非線形バネから成る1次元の準結晶モデルを利用し、数値計算を行う。 フリップが起こる割合や、フリップが起こるときに与える影響を調べる。 （本研究でのモデルでは、短距離の秩序が保たれるようにポテンシャルを与えている。 実際は、長距離に渡る秩序を議論すべきであると思っている。）